https://www.acmicpc.net/problem/2748
2748번: 피보나치 수 2
문제 피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n>=2)��
www.acmicpc.net
동적계획법(Dynamic Programmin)이란 복잡한 문제를 작은 단위로 분할하여 풀고 최종적으로 그것을 결합해 해겨하는 방법을 말한다.
동적계획법의 핵심은 메모이제이션(Memoization)이다.
동일한 계산이 중복되는 문제에서 한 번 계산한 결과는 저장해 둔다. 그리고 다음 번 동일한 계산이 필요할 때 연산하지 않고, 저장해둔 이전 결과에 접근해 사용하는 방식이다.
위 문제를 단순한 재귀 방식과 메모이제이션 방식으로 나누어 풀어보자.
1. 단순 재귀
# Fibonacci2.py
def Fibonacci(count):
if count < 2:
return li[count]
return Fibonacci(count - 1) + Fibonacci(count - 2)
n = int(input())
li = [0, 1]
print (Fibonacci())
기본적인 피보나치 수열을 구하는 방법이다.
위와 같은 재귀호출을 하게 되면 n = 4일 때, 다음과 같은 구조로 계산된다.
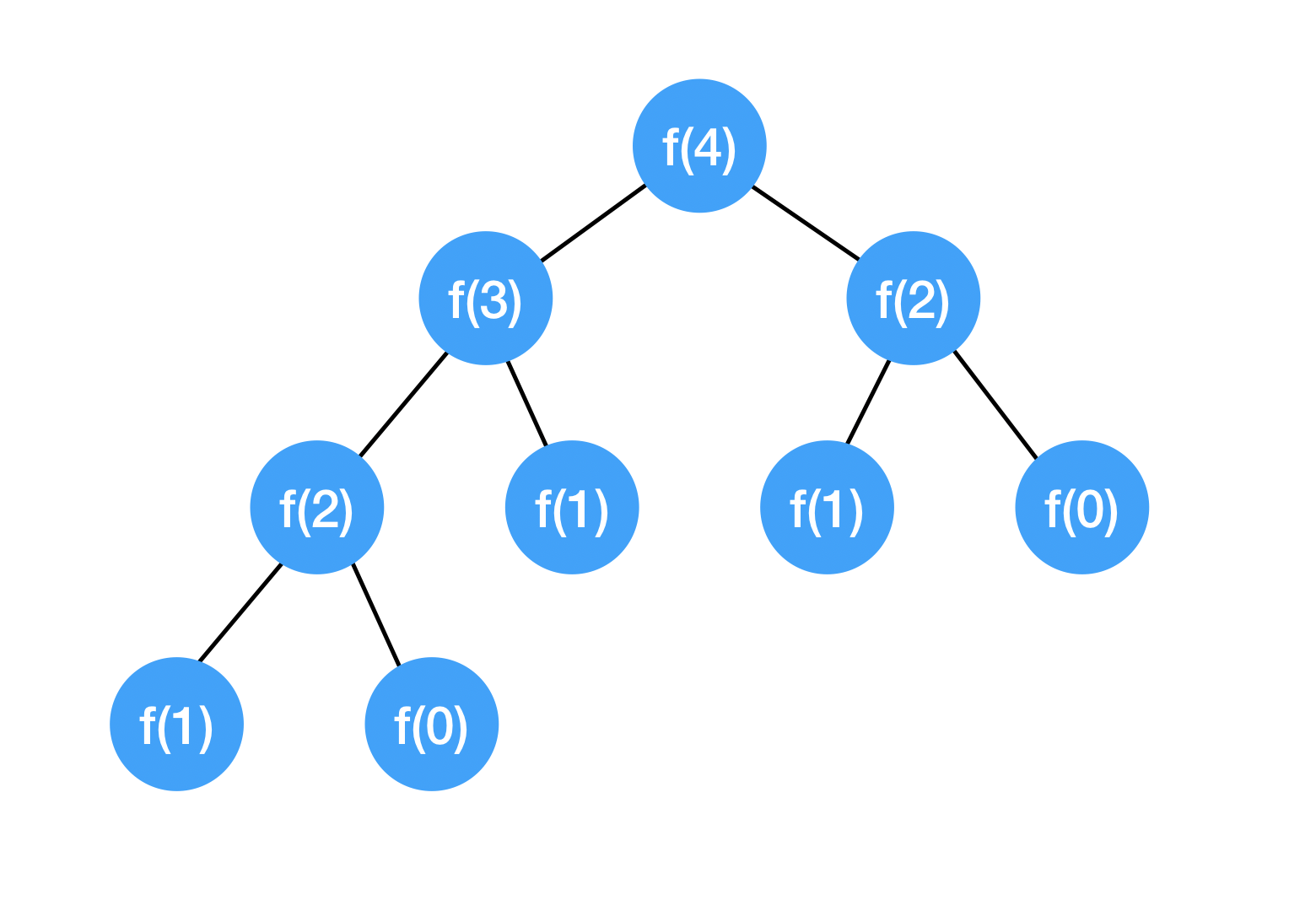
총 9번의 계산이 일어나고, 그 중 f(2)를 1번, f(1)을 2번, f(0)을 1번씩 중복 호출한다.
이런 방식으로 피보나치 수열을 구할 경우, 지수 함수의 시간 복잡도가 형성된다.
때문에 n값이 작을 때는 맞는 답이 나오지만 시간 초과로 문제를 해결할 수 없다.

2. 메모이제이션
#Fibonacci2.py
def Memozation():
for count in range(2, n + 1):
li.append(li[count - 1] + li[count - 2])
n = int(input())
li = [0, 1]
Memozation()
print (li[n])
리스트에 한 번 구한 답을 계속 저장하면서 다음 값을 구하는 방식이다.
시간 복잡도는 O(N)이 된다.
결과도 잘 나온다.

'알고리즘 문제풀이(Python)' 카테고리의 다른 글
| 1003번: 피보나치 함수 - 동적계획법 (0) | 2020.07.19 |
|---|---|
| 10816번: 숫자 카드 2 - Hash Table (0) | 2020.07.01 |
| 10816번: 숫자 카드 2 - 이분 탐색(Lower Bound, Upper Bound) (0) | 2020.07.01 |